DataStructures

Arrays:

Collection of "Similar Type of Data Elements" stored in a "contiguous location".

Operations:

Case 1: Unsorted Array

Search:

a=[5 2 1 3 4 6 -2]

num = 5

nun index of num in a[] , if not found return -1

Approach: Traverse each value one by one and check if a[i == num Best case:O(1) , num == a[0] Worst Case: O(N), Element not found Operation Time Space

Search O(N) O(1) Insert Delete

SubArray: Contiguous Smaller Array of Large Array

a[] = [5,1,3,2,4,6] ex: [1,3] :YES , [1,3,2] :YES [1,3,4] : NO

SubSequence: Smaller Array from the Larger Array, Does not Necessarily Contiguous But ORDER must be maintained.

Eg: [1,3] :YES [1,3,2] : YES [1,3,4] : YES [1,3,6,4] : NO

SubSet: ANY COMBINATION Smaller Subset of Array. Does Not Necessarily Contiguous and Order Does not matter. Eg:

2D Arrays:

int[][] = new int[5][6];
Transpose of a matrix : you have a square 2d matrix.return the transpose of a given matrix. i.e convert all the columns into rows.

LinkedList

When the spaces are not available together we are not able to store in array with large size , it may throw throw stack over flow, and came up with Linked List.
So along with value we should store address of next node.

Add the element at the start:

  Node node = new Node(10);
  node.next = head
  head =node

Add the element at the end:

  Node temp = head;
  while(temp!=next){
  temp = temp.next; 
  }
  temp.next = node;
  node.next = null

Add the element in the middle: we need to pass the index

  Node temp = head;
  for(int i = 0 ; i<index-1;i++){
  temp = temp.next;
  }
  Node temp1 = temp.next;
  Node temp2 = temp1.next;
  temp1.next = node;
  node.next = temp2;

Stack

In dynamic array we can add element at any index , but if I restrict the operations to add at last and remove at last.This data structure is known as Stack.
This will automatically follow LIFO (last in first out).
For example you are elements into stack 10 20 30 40 50
It will look like 50 40 30 20 10
If you want to remove element, you can only remove 50. Now the stack looks like 40 30 20 10 , now if we remove again we will get 40.
push() --> to add an element.
peek() --> get the top element.
size() --> size of the stack.
pop() ---> remove the element.

Queue

Add at end, but remove from first.
FIFO(first in first out).
offer() --> to add the element.

Tree

If you want to store hierarchical data.
Nomenclature in tree:

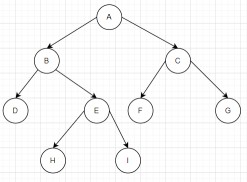
root node - the top most node of the hierarchy.
parent node - here B, E,C are the parent node.
child node - successors of given node.
child node(C) -F ,G
child node(B) - D,E
siblings - nodes with common parent.
leaf node - nodes with zero children.
ascendants - all the nodes above that given node. For ex: ascendants of I - E,B,A (root node)
descendants - all the nodes below the given node.
Height of a node: take out the path from that given node to all other leaf nodes. length in terms of edge.
Height of A:
1. A-C-F (2) 2. A-C-G(2) 3. A-B-E-I (3) 4. A-B-D-H(3)
we need to consider maximum length as the height of the node. So here the maximum length is 3.
Depth of Node:take out the path from that root node to the that node.

Heap

Priority Queue: removes highest priority element. gives prior to lower value if its default priority queue. 50 10 20 30 70 remove() - 10

HashMap

India -138 Pakistan - 22 Nepal - 3 USA -33 key -value pair

HashSet

duplicates will not be added
only keys in map will be added as values in set.

Graphs

It is nothing but collection of nodes, connected to each other using edges.

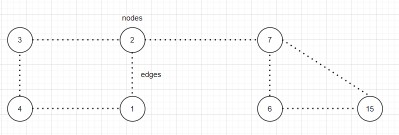
Real Time Examples: 1. Facebook friends 2. Google Maps

Trees vs Graphs

In trees there is a unique node which is known as root. , in graphs no unique node which is known as root.
Hierarchy is clearly defined . no hierarchy in graphs.
Treed cannot form a cycle. Graphs can form cycle.

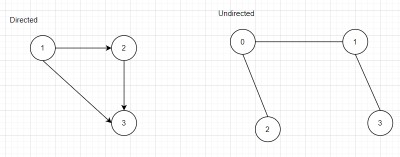
Classification of graphs: Case 1 : Directed and Undirected.

Case 2 :

Case 3:

Undirected Cyclic growth and Undirected Acyclic graph

Case 4 : Directed Cyclic and Directed Acyclic graph

Input of a Graph: assume graph is undirected . the first line will have 2 integers one is no.of nodes and other is no. of edges.

7 8

0 1

0 3

1 2

3 2

3 4

6 5

4 5

Dynamic Programming

Optimization over recursion.
Storing the results of previous states.
Those who don't remember the past are commended to repeat it.
Overlapping sub problem
1. Top down approach -- recursive (memoization / keep in memory (arrays , hashmaps))
1. Bottom up approach -- iterative

Greedy:

Find me the BEST Solution Now.
DON'T THINK FOR FUTURE.

BackTracking

(true or false) (0 or 1) (possible or not possible)

Optimisation Over Brute Force (Exhaust All possible options)

state space tree

Hashing: 1.Encryption and decryption are both are part of hashing. 2.shortening url 3.cryptography algos : sha 256,md5,rsa

Rolling Hash KMP/Rabin Karp - String matching Algos

Prime Number: Efficient Hash Function P = 10^9+9 h() = s[0]+(pi+pi^2+p*i^3...) mod p